Skip to main content

Section 9.1 Fourier Series Motivation

When I ask a room full of students to sketch an example of a periodic function, at least half will draw a sine or cosine. This is a great choice in the sense that sines and cosines are particularly simple and easy to deal with algebraically. (Even easier are complex exponentials--more about this later.) However, there are many other periodic functions that are not so simple. These functions can represent oscillatory phenomena that occur in so many places in nature. But, fortunately for us, it turns out that we can express all periodic phenomena as sums (possibly infinite sums) of sines and cosines. These sums are called Fourier Series.

Here is the basic formula for a Fourier series for the periodic function \(f(x)\text{:}\)

\begin{equation} f(x)=\frac{a_0}{2} +\sum_{n=1}^{\infty}a_n\,\cos{nx}+\sum_{n=1}^{\infty}b_n\,\sin{nx}\label{eq-fourier}\tag{9.1.1} \end{equation}

The coefficients \(a_n\) and \(b_n\) depend on \(f(x)\text{.}\) The formulas for finding the coefficients for a given \(f(x)\) can be found in Section 9.5 The geometric idea behind the formulas for the coefficients can be found in Section 9.4.

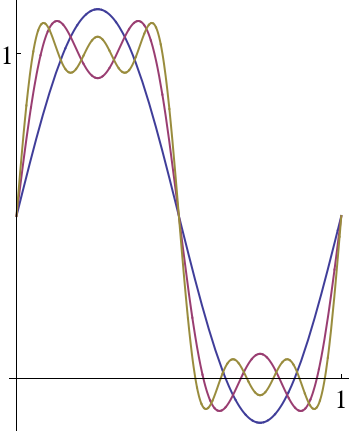
Fourier Series are most often used to approximate a function by giving the first few terms. In Figure 9.1.1 you can see how well the first few terms approximate a step function.

Figure 9.1.1. The first few partial sums in the Fourier series for a step function.

login