Section 11.4 Curvature
¶The classic models of non-Euclidean geometry are the sphere and the Poincaré disk, which, as we have seen can also be represented as a hyperboloid in Minkowski space. These three models – one Euclidean, one elliptic, and one hyperbolic – have one thing in common: They all have constant curvature.
The Euclidean plane is flat, that is, it has zero curvature. The sphere has constant positive curvature. The hyperboloid has negative curvature; unlike the sphere, it curves one way in one direction, and the other way in the other direction. In this respect, the hyperboloid is analogous to a saddle, which also has negative curvature. Although not immediately obvious, the hyperboloid has constant negative curvature.
However, this hyperboloid lives in Minkowski space. Is there a Euclidean surface with constant negative curvature? In fact there is. This surface is the pseudosphere, and is the surface of revolution obtained from a tractrix, both of which are shown in Figure 11.4.1.

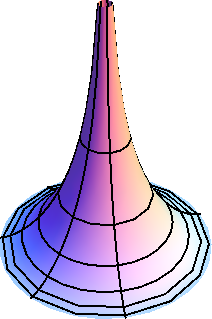
So we now have objects in (three-dimensional) Euclidean space that are both flat and curved. But Minkowski space itself turns out to be flat! Are there curved analogs of Minkowski space? Yes, indeed – and that is the geometric arena for general relativity!
The study of such models is called differential geometry. As shown in Table 11.4.2 these models can be classified by whether they are flat or curved, and whether their distance function is positive-definite or has one (or more!) timelike directions.
| flat | curved | |
| space | Euclidean | Riemannian |
| spacetime | Minkowskian (SR) | Lorentzian (GR) |