Double Integrals in Polar Coordinates

Section 5.10 Double Integrals in Polar Coordinates

Suppose you want to find the total mass of a round flat plate? How do you chop a round region?

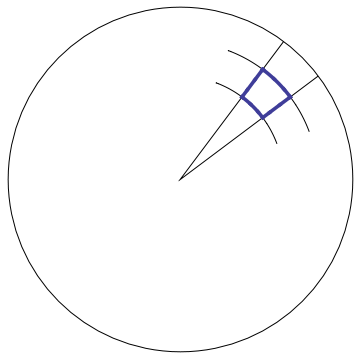
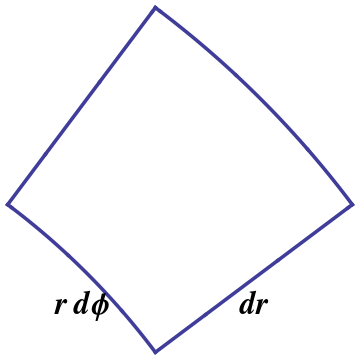
Figure 5.10.1. Chopping a circular region.

Figure 5.10.2. An infinitesimal box in polar coordinates.

When working with round regions, it usually helps to use round coordinates! In polar coordinates, one chops a region into pie shaped regions using radial lines and circles, as shown in Figure 5.10.1. These lines are orthogonal to each other, so that a small enough piece is nearly rectangular, which means that its area is just its length times its width. As shown in Figure 5.10.2, a little thought shows that a radial side has length \(dr\text{,}\) but a circular side has length \(r\,d\phi\) — not merely \(d\phi\text{,}\) which has the wrong units. Thus, in polar coordinates, ¹

\begin{equation} dA = r \,dr \,d\phi .\tag{5.10.1} \end{equation}

Expressing the mass density in terms of polar coordinates, \(\sigma=\sigma(r,\phi)\text{,}\) then yields the total mass in the form

\begin{equation} M = \int \sigma\,dA = \dint \sigma(r,\phi) \> r\,dr\,d\phi .\tag{5.10.2} \end{equation}

For a round plate, the limits on this integral will be constant. The integral will be especially simple to evaluate if the density function is also round, that is, if \(\sigma=\sigma(r)\) does not depend on \(\phi\text{.}\)

Perhaps surprisingly, there is no reasonable sense in which the infinitesmal rectangular and polar pieces have “the same” area. Rather, you must decide from the beginning how you wish to chop things up, relying on the fact that it won't affect the final answer.

For example, suppose that the density is given by \(\sigma=kr^2\text{,}\) with \(k\) constant. Then the mass of a circular plate of radius \(R\) is

\begin{gather*} M = \int_0^{2\pi} \int_0^R kr^2 r\,dr\,d\phi = (2\pi) k \left(\frac{R^4}{4}\right) = \frac{k\pi R^4}{2} . \end{gather*}